Skip to content

Math

Get digits of a number

  1. Use modulo 10 to extract last digit
  2. Update n by subtracting last digit
  3. Divide n by 10 (shifts penultimate digit to last)
  4. Repeat until n = 0
n = 123
digits = []
while True:
    remainder = n % 10
    digits.append(remainder)
    n -= remainder
    if n == 0:
        break
    n = n // 10
# digits: [1, 2, 3]

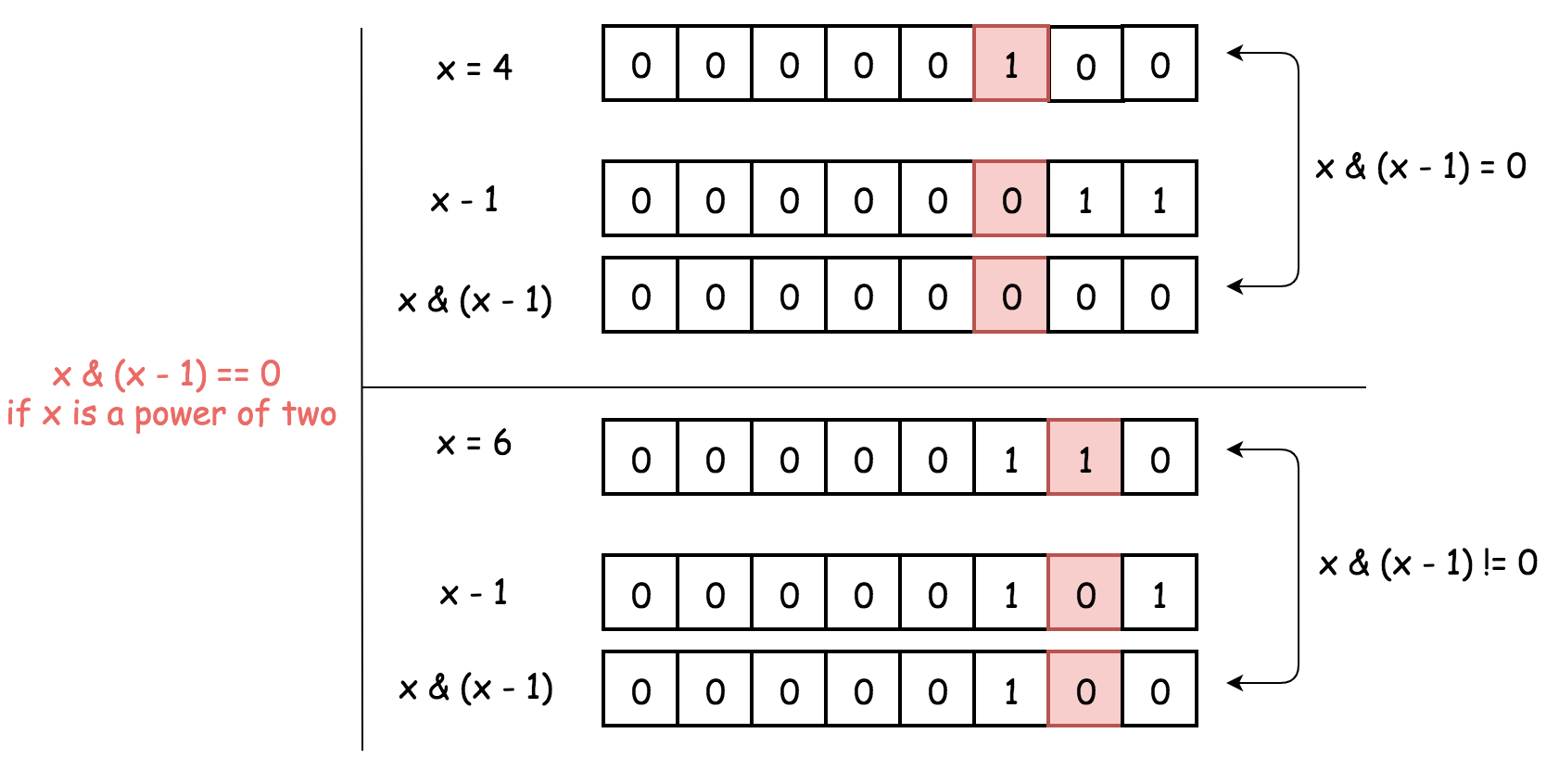
Check if number is a power of two

Given an integer n, return true if it is a power of two. Otherwise, return false.

Note

An integer n is a power of two, if there exists an integer x such that \(n = 2^x\). Example: \(2, 4, 8, 16, \dots\)

One could attempt to divide a number by two until you reach 1. If you do, it is a power of 2. This is around \(\mathcal{O}(logn)\) in Time Complexity.

More efficient is to use bitwise operator. The following tricks are at our disposal:

  • How to get / isolate the rightmost 1-bit: n & (-n).
  • How to turn off (= set to 0) the rightmost 1-bit: n & (n - 1).

These two tricks are also used in the N-Queens Problems.

def isPowerOfTwo(self, n: int) -> bool:
    if n <= 0:
        return False
    return n & (n - 1) == 0

Time Complexity: \(\mathcal{O}(1)\)

Space Complexity: \(\mathcal{O}(1)\)

Power of 2

Check if a Palindrome

Note

An integer is a palindrome when it reads the same forward and backward.

Intuition is based on getting the digits of a number. Albeit one could also use string representation of a number.

  1. Use modulo 10 to extract last digit. Add to reverse (initially 0)
  2. Update n by subtracting last digit
  3. Divide n by 10 (shifts penultimate digit to last), multiply reverse by 10.
  4. Repeat until n = 0
  5. If reverse equal original n then n is palindrome.
def isPalindrome(x: int) -> bool:
    if x < 0:
        return False
    n = x
    reverse = 0
    while x > 0:
        remainder = x % 10
        reverse = (reverse * 10) + remainder
        x = x // 10
    return n == reverse

Happy Number

A happy number is a number defined by the following process:

  • Starting with any positive integer, replace the number by the sum of the squares of its digits.
  • Repeat the process until the number equals 1 (where it will stay), or it loops endlessly in a cycle which does not include 1.
  • Those numbers for which this process ends in 1 are happy.
def isHappy(n: int) -> bool:
    if n < 0:
        return False
    previous = []
    while True:
        val = n
        digits = []
        while True:
            remainder = val % 10
            digits.append(remainder ** 2)
            val -= remainder
            if val == 0:
                break
            val = val // 10
        n = sum(digits)
        if n == 1:
            return True
        elif n in previous:
            return False
        previous.append(n)
    return False

Find the digit that occurs only once

Given a non-empty array of integers nums, every element appears twice except for one. Find that single one.

Using bitwise manipulation with XOR, we can implement a solution with a linear runtime complexity and use only constant extra space.

  • If we take XOR of zero and some bit, it will return that bit. \(a \oplus 0 = a\)
  • If we take XOR of two same bits, it will return 0. \(a \oplus a = 0\)
  • Thus: \(a \oplus b \oplus a = (a \oplus a) \oplus b = 0 \oplus b = b\)
nums = [...] # list of integers such as [1,1,2,3,3]
a = 0
for n in nums:
    a ^= n
return a

Reverse a binary number

Given a (binary) number representation of size power (e.g., 4 bit), reverse it so the bits are in reverse order.

  • We iterate through the bit string of the input integer, from right to left (i.e. n = n >> 1). To retrieve the right-most bit of an integer, we apply the bit AND operation (n & 1).
  • For each bit, we reverse it to the correct position (i.e. (n & 1) << power). Then we accumulate this reversed bit to the final result.
  • When there is no more bits of one left (i.e. n == 0), we terminate the iteration.

The complexity is \(\mathcal{O}(1)\) for space and time as we iterate always on a fixed size.

def reverseBits(n: int) -> int:
    print(n, bin(n))
    print('-'*20)
    ret, power = 0, 3
    while n:
        print(n, bin(n), ret, bin(ret))
        ret += (n & 1) << power
        n = n >> 1
        power -= 1
    print('-'*20)
    print(ret, bin(ret))
    return ret

>>> reverseBits(n=11)
11 0b1011
--------------------
11 0b1011 0 0b0
5 0b101 8 0b1000
2 0b10 12 0b1100
1 0b1 12 0b1100
--------------------
13 0b1101
13

Calculate the Square Root of X

There are various ways to take the square root of X. One of which being to calculate \(X^{\frac{1}{2}}\). But there are also algorithmic versions. Such as the Babylonian Method (aka Heron's Method) or Newton's Method.

  • Take a guess of what the square root might be. A square root is always between \(0\) and \(\frac{X}{2}\). So, \(\frac{X}{2}\) might be a good starting point.
  • Update the guess by the average of \(X\) and the previous guess.
  • Run until desired precision is reached.

Newtons method has a similar intuition than the babylonian method. It is widely used today. It can also be used to take other roots than just the square root.

Babylonian Method:

def babylonianmethod(x: int) -> int:
    if x == 1:
        return 1
    epsilon = 0.001  # precision
    guess = x // 2   # the sqrt is always smaller than x/2
    while guess > 0:
        guess = (guess + (x / guess)) / 2
        # check if we should stop
        if abs(guess**2 - x) <= epsilon:
            break
    return guess

Newton's Method: 

def newtonsmethod(x: int) -> int:
    if x < 2:
        return x

    x0 = x
    x1 = (x0 + x / x0) / 2
    while abs(x0 - x1) >= 1:
        x0 = x1
        x1 = (x0 + float(x) / x0) / 2

    return x1

Fibonacci Sequence

You are climbing a staircase. It takes n steps to reach the top. Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?

\[Fib(n) = Fib(n-1) + Fib(n-2)\]

Binets Method is a version of the Fibonacci sequence using matrix multiplication.

def fib(n: int) -> int:
    a, b = 0, 1
    i = 1
    while i < n:
        a, b = b, a + b
        i += 1
    return a + b

Tribonacci is a special case where the following formula applies:

\[ T_0 = 0, T_1 = 1, T_2 = 1 \]

and

\[ T_{n+3} = T_n + T_{n+1} + T_{n+2} \]

for

\[ n >= 0 \]
def tribonacci(n: int) -> int:
    a, b, c = 0, 1, 1
    if n < 3:
        return [a, b, c][n]
    i = 3
    while i < n:
        a, b, c = b, c, a + b + c
        i += 1
    return a + b + c

The algorithm above has \(\mathcal{O}(n)\) time complexity and \(\mathcal{O}(1)\) space complexity.

Factorial

\[n! = n \times (n-1) \times \dots \times 1\]

def factorial(num):
    a, b, i = 1,2,2 # base cases and our i counter.
    while i < num: # if i is equal to num, we're done, last product will be at return.
        c = a * b # start to multiply and save in c.
        i+=1 # add 1 to i because we want to multiply next number with c (in the next iteration).
        a, b = c, i # update variables to the next iteration.
    return a * b if num > 1 else 1 # last product occurs here is num is greater than 1.
(Note: Can also be used for Fibonacci)

Count trailing zeros of a factorial

Given an integer n, return the number of trailing zeroes in n!.

def factorial(num):
    a, b, i = 1,2,2 # base cases and our i counter.
    while i < num: # if i is equal to num, we're done, last product will be at return.
        c = a * b # start to multiply and save in c.
        i+=1 # add 1 to i because we want to multiply next number with c (in the next iteration).
        a, b = c, i # update variables to the next iteration.
    return a * b if num > 1 else 1 # last product occurs here is num is greater than 1.

def trailingZeroes(n: int) -> int:
    res = factorial(n)
    tz = 0
    while True:
        if res % 10 == 0:
            tz += 1
            res = res // 10
        else:
            break
    return tz

Trailing zeros in a factorial come from multiplying pairs of 2 and 5. Since factors of 2 are more frequent, we only need to count the number of 5s in the prime factorization of n!.

  1. Initialize count to 0 and divisor to 5.
  2. While n is greater than or equal to divisor:
    • Add n // divisor to count.
    • Multiply divisor by 5.
  3. Return the count, which represents the number of trailing zeroes in n!.

Complexity:

  • Time: \(\mathcal{O}(\log_{5}(n))\) since \(n\) is divided by \(5\).
  • Space: \(\mathcal{O}(1)\) constant space
def trailingZeroes(n):
    count = 0
    divisor = 5

    while n >= divisor:
        count += n // divisor
        divisor *= 5

    return count

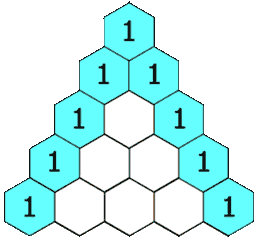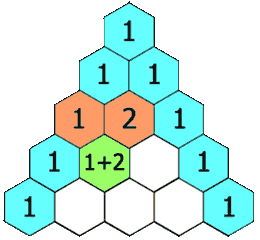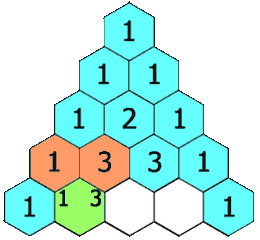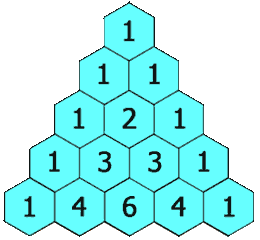
Pascal's Triangle

Define an algorithm for the Pascal's Triangle which constructs the triangle.

Trie

We could be using Binomial Coefficients to derive the values. However, this algorithm would be \(\mathcal{O}(n^3)\) complexity.

Time Complexity: \(\mathcal{O}(n^2)\) Space Complexity: \(\mathcal{O}(n^2)\)

def generate(numRows: int) -> List[List[int]]:
    rows = []
    for i in range(1, numRows + 1):
        to_insert = [1]*i
        if i != 1: # not the first row
            to_fill = i - 2 # minus start and end
            prev_row = rows[-1] # get previous row
            for l, t in zip(range(len(prev_row)-1), range(1, to_fill+1)):
                r = l+1
                to_insert[t] = prev_row[l] + prev_row[r]
        rows.append(to_insert)
    return rows

Binomial Coefficients

TODO

Greatest Common Divisor (GCD) / Euclidean Algorithm

def gcd(a: int, b: int):
    while b:
        a, b = b, a % b
    return a

def gcdOfStrings(str1: str, str2: str) -> str:
    # Check if they have non-zero GCD string.
    if str1 + str2 != str2 + str1:
        return ''
    # Algorithm
    while len(str2) > 0:
        str1, str2 = str2, str1.replace(str2, '')
    return str1

Digital Root (aka repeated digital sum)

Given an integer num, repeatedly add all its digits until the result has only one digit, and return it.

This problem can be solved either algorithmically or mathematically by using the digital root trick.

def addDigits(num: int) -> int:
    def get_digits(number):
        digits = []
        current = number
        while True:
            if current == 0: 
                break
            digit = current % 10
            digits.append(digit)
            current = (current - digit) // 10
        return digits
    ans = num
    while ans >= 10:
        ans = sum(get_digits(ans))
    return ans

Time Complexity: \(\mathcal{O}(logN)\)

Space Complexity: \(\mathcal{O}(logN)\)

One can solve it using the following formula:

\[ f(n) = \begin{cases} 0 & \quad \text{if } n \text{ = 0}\\ 1 + (n-1) \% 9 & \quad \text{otherwise} \end{cases} \]
def addDigits(num):
    if num == 0:
        return 0
    return 1 + (num - 1) % 9

Time Complexity: \(\mathcal{O}(1)\)

Space Complexity: \(\mathcal{O}(1)\)

A more general version of the formula is applicable for any base \(b\).

\[ {dr}_{b}(n)={\begin{cases}0&{\mbox{if}}\ n=0,\\1\ +\ ((n-1){\bmod {(b-1)}})&{\mbox{if}}\ n\neq 0.\end{cases}} \]