Data Structures¶
NLP¶
Ngrams¶
An n-gram is a sequence of n adjacent symbols in particular order.
Linked Lists¶
Single-linked list¶
Definition¶
Cycle Detection¶
The Floyd Algorithm aka Slow Fast Algorithm solves this problem.
- We use two pointers in the linked list.
- We traverse the linked list with both of the pointers.
- The first pointer advances two steps each time, and the other one step. They advance alternating.
- If at any point the "slower" pointer is in the next two fields of the "faster" pointer, the linked list has a cycle.
- Otherwise if the "faster" reaches the end of the linked list (next is empty), then there is no cycle.
def hasCycle(head: Optional[ListNode]) -> bool:
if head is None:
return False
slow = head
fast = head
while True:
# advance fast 2 steps
if fast.next is not None:
if fast.next == slow:
return True
if fast.next.next is not None:
if fast.next.next == slow:
return True
fast = fast.next.next
else:
return False
else:
return False
# advance slow 1 step
if slow.next is not None:
slow = slow.next
else:
# unlikely case
return False
Sorting¶
Sorting a linked list efficiently requires avoiding random access, which makes merge sort the ideal choice. It’s a classic example of applying divide-and-conquer where understanding node splitting and merging is key.
- Use the fast and slow pointer technique to split the list into two halves.
- Recursively sort each half.
- Merge the sorted halves using a helper function.
- Time: \(\mathcal{O}(n\log(n))\) (due to merge sort)
- Space: \(\mathcal{O}(\log(n))\) (due to recursive stack space)
Reverse¶
Given the head of a singly linked list, reverse the list, and return the reversed list.
- Put each next element in front of the current head.
- Take previous next, which is now in front, as the new head.
- Continue with the next of previous next and repeat process.
- Time: \(\mathcal{O}(n)\) (due to going through the list once)
- Space: \(\mathcal{O}(1)\) (no additional storage)
def reverseList(head: Optional[ListNode]) -> Optional[ListNode]:
if not head:
return
# Allocate new_head pointer
new_head = head
# Set working item to the next element (if this is not none we will put it infront of current head)
current = head.next
# Set original next of head to None to finish up list.
new_head.next = None
while current:
# Grab next of current (we will use it later to continue)
orig_next = current.next
# Put current in front of head and let it point to previous head
current.next = new_head
new_head = current
# Take original next as current to continue
current = orig_next
return new_head
The difference to the whole list is that we only start after left amount of steps have been made through the linked list and only for right-left steps. For this sublist/slice, we will apply the exact same function as for the whole list. After that there is boilerplate to interweave the reversed list again. Complexities are identical.
def reverseBetween(head: Optional[ListNode], left: int, right: int) -> Optional[ListNode]:
if not head:
return
if not head.next:
return head
if left - right == 0:
return head
def find_idx(ptr, i):
idx = 1
pos = ptr
prev = None
while pos:
if idx == i:
break
prev = pos
pos = pos.next
idx += 1
return pos, prev
# find left node
l, lprev = find_idx(head, left)
# find right node
r, _ = find_idx(l.next, right - left)
# store tail for later use
tail = r.next
# reverse
new_head = reverseList(head=l, limit=right-left)
# interweave reversed
if lprev:
# we are not at the beginning of the list
lprev.next = new_head
else:
head = new_head
end_of_reversed = new_head
while end_of_reversed:
previous_end = end_of_reversed
end_of_reversed = end_of_reversed.next
previous_end.next = tail
return head
def reverseList(head: Optional[ListNode], limit: int) -> Optional[ListNode]:
if not head:
return
# Allocate new_head pointer
new_head = head
# Set working item to the next element (if this is not none we will put it infront of current head)
current = head.next
# Set original next of head to None to finish up list.
new_head.next = None
counter = 0
while current:
if counter >= limit:
break
# Grab next of current (we will use it later to continue)
orig_next = current.next
# Put current in front of head and let it point to previous head
current.next = new_head
new_head = current
# Take original next as current to continue
current = orig_next
counter += 1
return new_head
Rotate Linked List¶
Given the head of a linked list, rotate the list to the right by k places.
To rotate a linked list, we effectively shift the last k nodes to the front. But instead of re-linking each node manually, we can form a cycle and break it at the right place. Also, rotation instructions (k) larger than the length of the list is redundant and can arithmatically be optimized using modulo.
- Count the length of the list. Optimize k.
- Connect the tail to the head to form a cycle.
- Find the new tail: (length - k % length) steps from head.
- Break the cycle and return the new head.
- Time: \(\mathcal{O}(n)\) (Single pass to count and another to break rotation.)
- Space: \(\mathcal{O}(\log(n))\) (No extra space used.)
def rotateRight(head: Optional[ListNode], k: int) -> Optional[ListNode]:
if head is None:
return
current = head
# Find end
n = 1
while current.next:
current = current.next
n += 1
# Optimize K -> no need to do it over and over again
k = k % n
if k == 0:
return head
# Circular linked list
current.next = head
# Advance k steps and break circular linked list
prev = current
current = head
to_advance = n - k # we basically need to step back, so since we do not have a double linked list, we need to advance but only enough.
for _ in range(to_advance):
prev = prev.next
current = current.next
prev.next = None
return current
Remove nth element from end¶
To remove the N-th node from the end, you'd normally think of counting the list size first — but that takes two passes. There's a smarter way: use two pointers, one shifted ahead by n.
- Add a dummy node before the head to handle edge cases (e.g. removing head).
- Move a
fastpointernsteps forward. - Move both
fastandslowtogether untilfasthits the end. slowwill be just before the node we want to remove — adjust its.next.
- Time: \(\mathcal{O}(L)\) single traversal of the list of
Lnodes. - Space: \(\mathcal{O}(1)\) (No extra space used.)
def removeNthFromEnd(head: Optional[ListNode], n: int) -> Optional[ListNode]:
dummy = ListNode(-1, head)
fast = slow = dummy
# Advance fast by n+1 steps (this will make slow stop before the nth node from the end)
for _ in range(n+1):
fast = fast.next
# Iterate linked list
while fast:
fast = fast.next
slow = slow.next
# "Remove" nth node
slow.next = slow.next.next
return dummy.next
Remove duplicate values from linked list (not deduplication!)¶
Given the head of a sorted linked list, delete all nodes that have duplicate numbers, leaving only distinct numbers from the original list. Return the linked list sorted as well.
- We use a dummy node to handle edge cases near the head. Then we iterate with two pointers:
prevtracks the last node before the duplicate sequence.currentmoves forward, skipping all nodes with the same value.
- If a duplicate sequence is detected, we skip it entirely by adjusting prev.next.
- Time: \(\mathcal{O}(n)\) each node is visited once.
- Space: \(\mathcal{O}(1)\) no extra space used.
def deleteDuplicates(head: Optional[ListNode]) -> Optional[ListNode]:
if not head or not head.next:
return head
dummy = ListNode(0, head)
prev = dummy
current = head
while current:
is_duplicate = False
# flag any as duplicate that have the same value twice after each other
# this allows us to iteratively advance and remove duplicates
while current.next and current.val == current.next.val:
is_duplicate = True
current = current.next
if is_duplicate:
prev.next = current.next
else:
prev = prev.next
current = current.next
return dummy.next
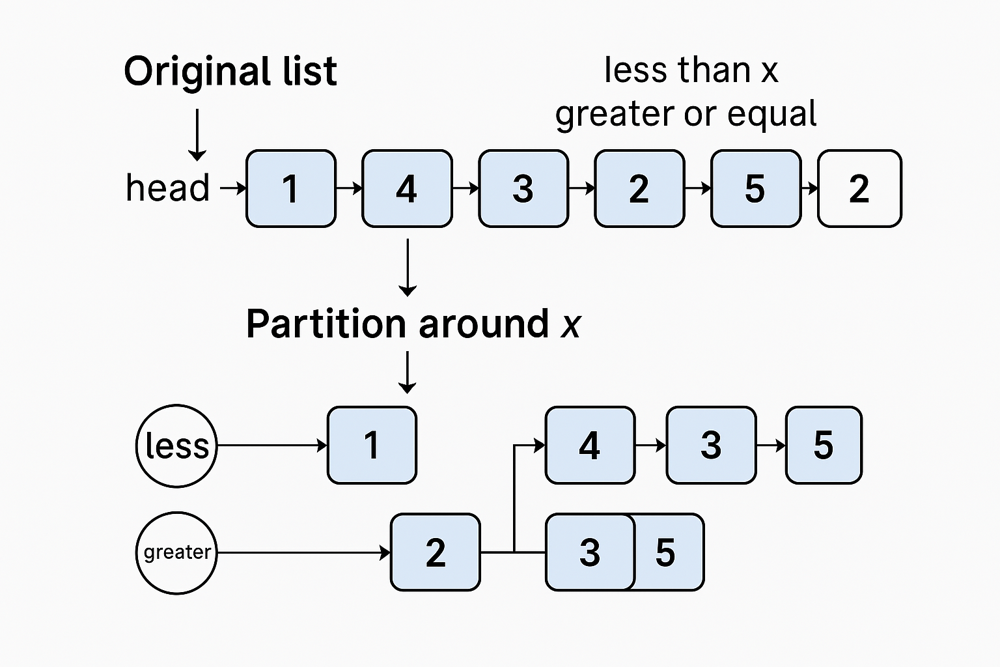
Partition and reorder Linked List by value¶
Given the head of a linked list and a value
x, partition it such that all nodes less than x come before nodes greater than or equal to x. You should preserve the original relative order of the nodes in each of the two partitions.
To rearrange a linked list around a pivot x, we separate nodes into two groups: those with values less than x and those greater or equal. Combining these gives the final partitioned list.
We use two dummy nodes to manage two separate lists: less for nodes with values less than x, and greater for the rest. Further, we track the tails of both lists. We iterate through the original list, linking nodes to the appropriate list. Finally, we connect less (without the dummy) to greater and return the new head.
- Time: \(\mathcal{O}(n)\) each node is visited once.
- Space: \(\mathcal{O}(1)\) no extra space used.
def partition(head: Optional[ListNode], x: int) -> Optional[ListNode]:
# track partition heads and tails
less = ListNode(0)
greater = ListNode(0)
lt = less
gt = greater
# iterate list and relink
while head:
if head.val < x:
lt.next = head
lt = lt.next
else:
gt.next = head
gt = gt.next
head = head.next
# unlink rest
gt.next = None
# merge tail of first partition to head of second partition
lt.next = greater.next
# return head
return less.next
Trees¶
Binary Tree¶
Definition¶
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
Traversal¶
The following general tree traversal are known. There is more (e.g., level-order) below. These ones are the general ones.
Find Max Depth¶
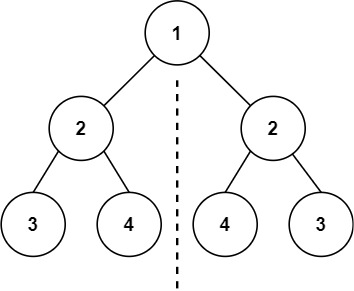
Is Tree Symmetric / Mirrored¶
class Algorithm:
def isSymmetricSubTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
# All of them are none.
if p is None and q is None:
return True
# One of them is null or not equal, so they aren't mirror images
if p is None or q is None or p.val != q.val:
return False
# Traverse down
return (
self.isSymmetricSubTree(p=p.left, q=q.right)
and self.isSymmetricSubTree(p=p.right, q=q.left)
)
def isSymmetric(self, root: Optional[TreeNode]) -> bool:
if root is None:
return True
return self.isSymmetricSubTree(p=root.left, q=root.right)
Complete Binary Tree¶
A complete tree is a binary tree were all nodes are filled except maybe the last one.
This check can "easily" be implemented in an array. The last layer k has 2^k elements.
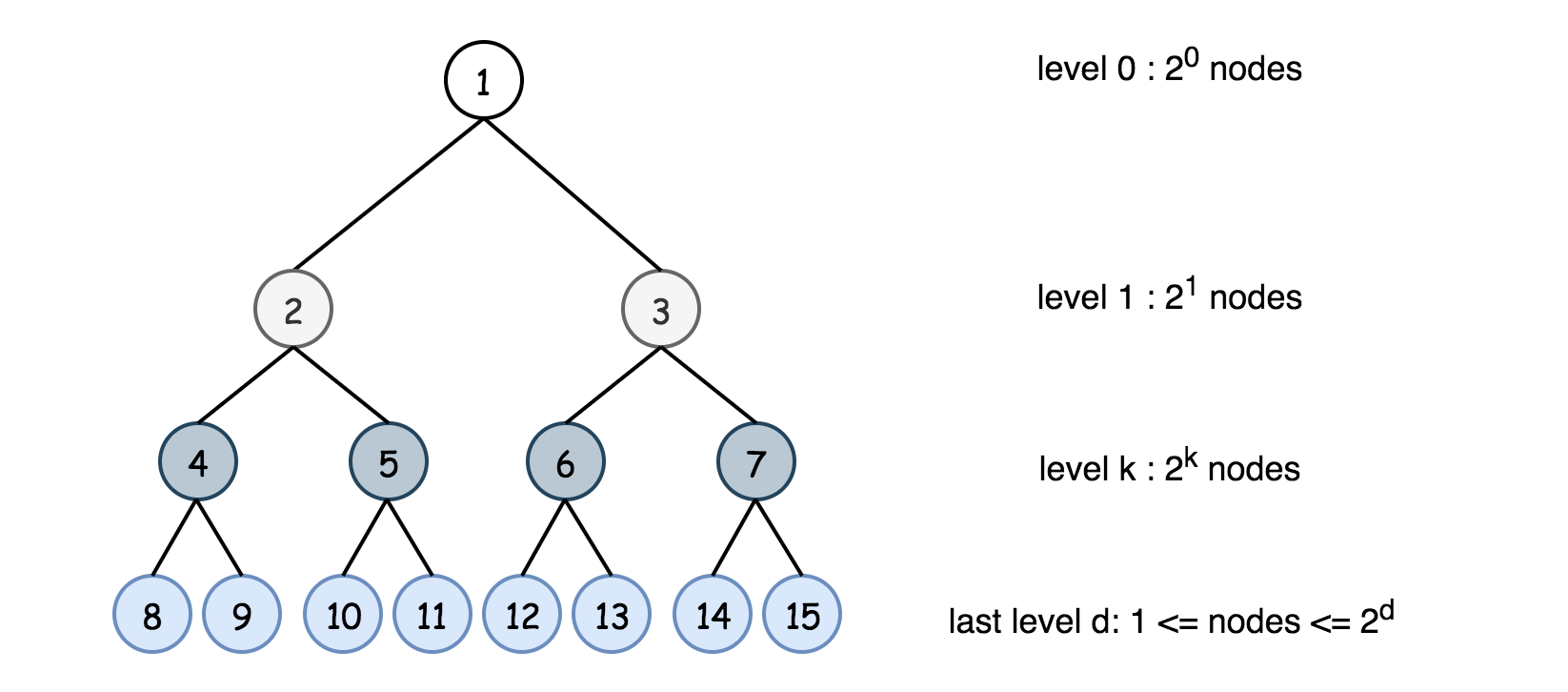
Let's assume the following tree:
graph TB;
A((1))-->B((2))
A-->C((3));
B-->E((4))
B-->F((5))
C-->H((6))
C-->I((7))Level-order Traversal¶
Given the root of a binary tree, return the average value of the nodes on each level in the form of an array.
- The idea is to use two queues to traverse in Level order manner. We will insert the first level in first queue and print it and while popping from the first queue insert its left and right nodes into the second queue. Now start printing the second queue and before popping insert its left and right child nodes into the first queue. Continue this process till both the queues become empty.
from collections import deque
def level_order_traversal_to_get_average_per_level(root: Optional[TreeNode]) -> List[float]:
result = []
if root is None:
return result
# Level Order Traversal
q_current = deque()
q_next = deque()
q_current.append(root)
# While queues are not empty
while q_current or q_next:
current_level_vals = []
# Take all elements from current queue and add their leafs to the next queue.
while q_current:
current = q_current.popleft()
current_level_vals.append(current.val)
if current.left is not None:
q_next.append(current.left)
if current.right is not None:
q_next.append(current.right)
# Storing current level into result
if current_level_vals:
result.append(current_level_vals)
current_level_vals = []
# Take all elements from current queue and add their leafs to the next queue.
while q_next:
current = q_next.popleft()
current_level_vals.append(current.val)
if current.left is not None:
q_current.append(current.left)
if current.right is not None:
q_current.append(current.right)
# Storing current level into result
if current_level_vals:
result.append(current_level_vals)
# Flatten
flat_result = []
for lvl in result:
flat_result.append(sum(lvl) / len(lvl))
return flat_result
Flatten a binary tree to a linked list¶
Given the root of a binary tree, flatten the tree into a "linked list": The "linked list" should use the same TreeNode class where the right child pointer points to the next node in the list and the left child pointer is always null. The "linked list" should be in the same order as a pre-order traversal of the binary tree.
Time Complexity: \(\mathcal{O}(n)\) each node is visited once. Space Complexity: \(\mathcal{O}(1)\) in place
def flatten(root: Optional[TreeNode]) -> None:
# start from the root
current = root
# for each node
while current:
# if a left child exists
if current.left:
# find the rightmost node in the left subtree
predecessor = current.left
while predecessor.right:
predecessor = predecessor.right
# connect its right to the current node's right
predecessor.right = current.right
# move the left subtree to the right and nullify the left pointer
current.right = current.left
current.left = None
# move to the next right node
current = current.right
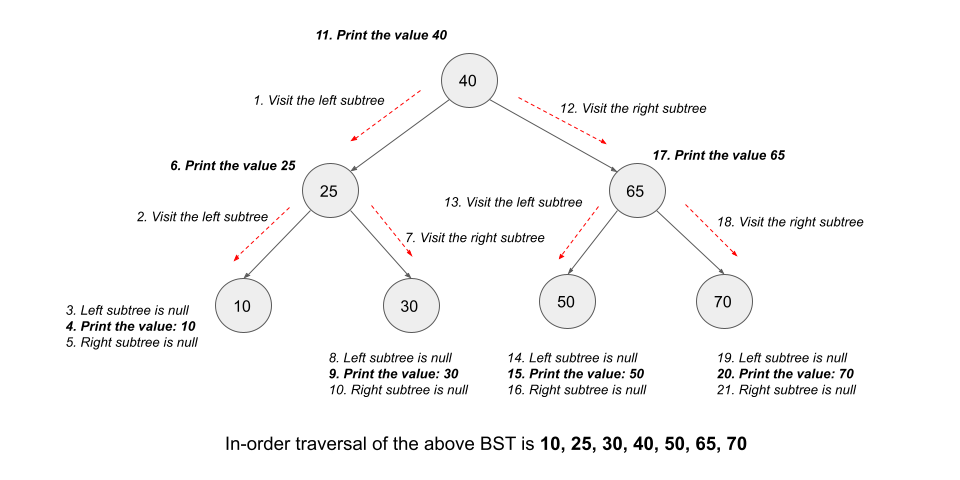
Binary Search Tree (BST)¶
Definition¶
A BST is a special form of a binary tree. A unique property of a binary search tree is that an inorder traversal handles the nodes in sorted order. This is due to the fact, that the left side of the node is always home of the values smaller than the node and the right side always home to the values larger than the node.
Find minimum difference of two adjacent nodes¶
Given the root of a Binary Search Tree (BST), return the minimum absolute difference between the values of any two different nodes in the tree.
Using inorder traversal, we can get a sorted list of the values of the tree in one pass. Hence, we would always only need to remember the value of the previous node in order to calculate the difference.
class Solution:
def getMinimumDifference(self, root: Optional[TreeNode]) -> int:
self.min_difference = float('inf')
self.prev = None
def inorder(node):
if node is None:
return
# left side
inorder(node.left)
# in
if self.prev is not None:
self.min_difference = min(self.min_difference, node.val - self.prev)
self.prev = node.val
# right side
inorder(node.right)
inorder(root)
return self.min_difference
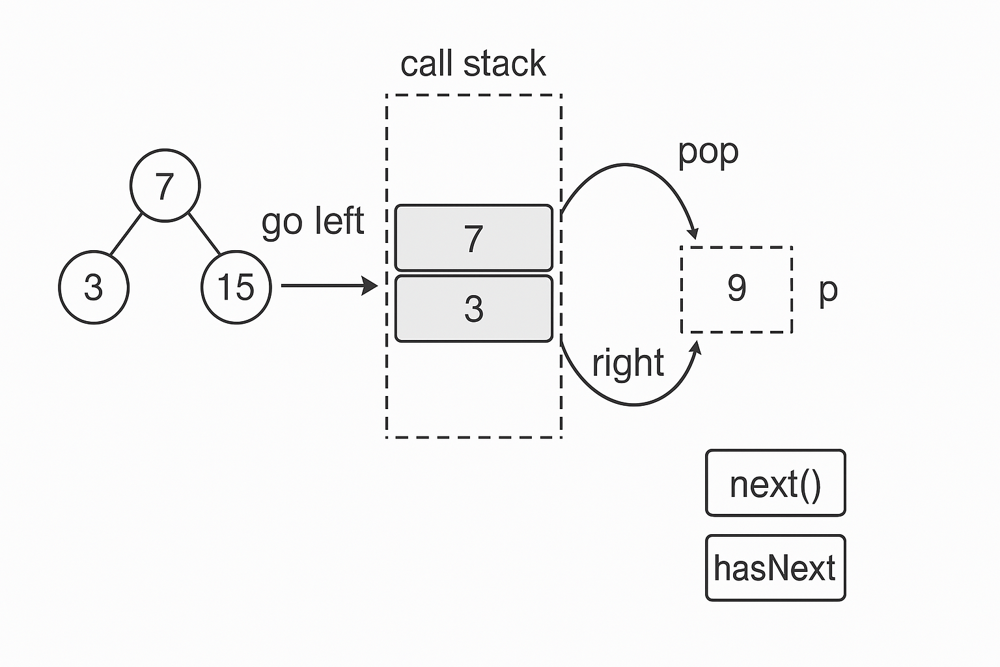
Iterator over a binary search tree (BST) in inorder traversal¶
Inorder traversal of a BST yields sorted elements. But generating the full list at once is wasteful. Instead, we use a stack to simulate the traversal and fetch elements one by one as needed.
- Use a stack to simulate recursion.
- Traverse left while pushing nodes onto the stack.
- When calling next(), pop the node and process its right subtree next.
- hasNext() checks if either the stack or the current pointer has nodes left to explore.
Time Complexity: \(\mathcal{O}(1)\) amortized over all next() calls Space Complexity: \(\mathcal{O}(h)\) for the height of the tree (for the stack)
class BSTIterator:
def __init__(self, root: Optional[TreeNode]):
self.stack = []
self.pointer = root
def next(self) -> int:
while self.pointer:
self.stack.append(self.pointer)
self.pointer = self.pointer.left
x = self.stack.pop()
self.pointer = x.right
return x.val
def hasNext(self) -> bool:
return len(self.stack) > 0 or self.pointer is not None
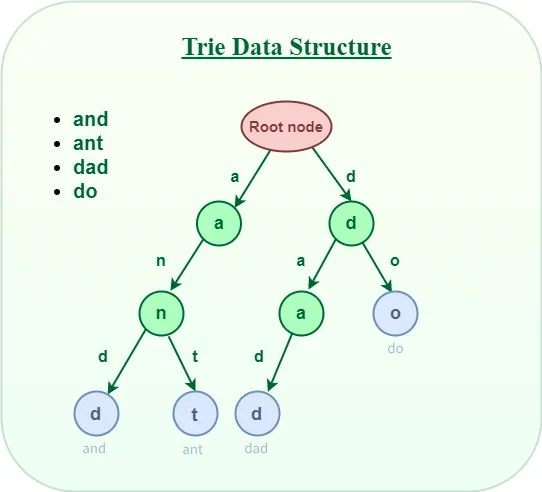
Trie¶
Definition¶
A trie (pronounced as "try") or prefix tree is a tree data structure used to efficiently store and retrieve keys in a dataset of strings.
Tries are particularly effective for tasks such as autocomplete, spell checking, and IP routing, offering advantages over hash tables due to their prefix-based organization and lack of hash collisions. A notable optimization is the radix tree, which provides more efficient prefix-based storage.
Implementation¶
class Trie:
class Node:
def __init__(self, val):
self.children = dict()
# Used as a flag to identify nodes that were at least once a terminal node - may at one point no longer be.
self.is_terminal = False
def __init__(self):
self.root = Trie.Node('')
def insert(self, word: str) -> None:
current = self.root
for i, character in enumerate(word):
if not current.children.get(character, None):
current.children[character] = Trie.Node(character)
current = current.children[character]
current.is_terminal = True
return
def _traverse(self, word):
current = self.root
for i, character in enumerate(word):
if not current.children.get(character, None):
return
current = current.children[character]
yield current
return
def search(self, word: str) -> bool:
prefix_parts = list(self._traverse(word=word))
prefix = ''.join(map(lambda x: x.val, prefix_parts))
prefix_exists = prefix == word
if len(prefix_parts) == 0:
return False
insertion_exists = prefix_parts[-1].is_terminal
return prefix_exists and insertion_exists
def startsWith(self, prefix: str) -> bool:
current = self.root
for i, character in enumerate(prefix):
if not current.children.get(character, None):
return False
current = current.children[character]
return True
class TrieNode:
def __init__(self):
self.children = [None] * 26 # Fixed size array for 'a' to 'z'
self.isEnd = False
class Trie:
def __init__(self):
self.root = TrieNode()
def insert(self, word: str) -> None:
node = self.root
for char in word:
index = ord(char) - ord('a')
if not node.children[index]:
node.children[index] = TrieNode()
node = node.children[index]
node.isEnd = True
def search(self, word: str) -> bool:
node = self.root
for char in word:
index = ord(char) - ord('a')
if not node.children[index]:
return False
node = node.children[index]
return node.isEnd
def startsWith(self, prefix: str) -> bool:
node = self.root
for char in prefix:
index = ord(char) - ord('a')
if not node.children[index]:
return False
node = node.children[index]
return True
class WordDictionary:
class TrieNode:
def __init__(self, val):
self.children = dict()
# Used as a flag to identify nodes that were at least once a terminal node - may at one point no longer be.
self.is_terminal = False
def __init__(self):
self.root = WordDictionary.TrieNode('')
def addWord(self, word: str) -> None:
current = self.root
for i, character in enumerate(word):
if not current.children.get(character, None):
current.children[character] = WordDictionary.TrieNode(character)
current = current.children[character]
current.is_terminal = True
return
def search(self, word: str) -> bool:
# recursion function to traverse the trie
def depthfirstsearch(node, i):
# check if we are at the end of our word
if i == len(word):
return node.is_terminal
# get current character of word
char = word[i]
# check if wildcard '.'
if char == '.':
# run for dfs for all children
return any(depthfirstsearch(child, i+1) for child in node.children.values())
# if not wildcard case return false if not in children
if char not in node.children:
return False
# for the non wildcard case, continue traversing
return depthfirstsearch(node.children[char], i+1)
# initiate traversal
return depthfirstsearch(self.root, 0)
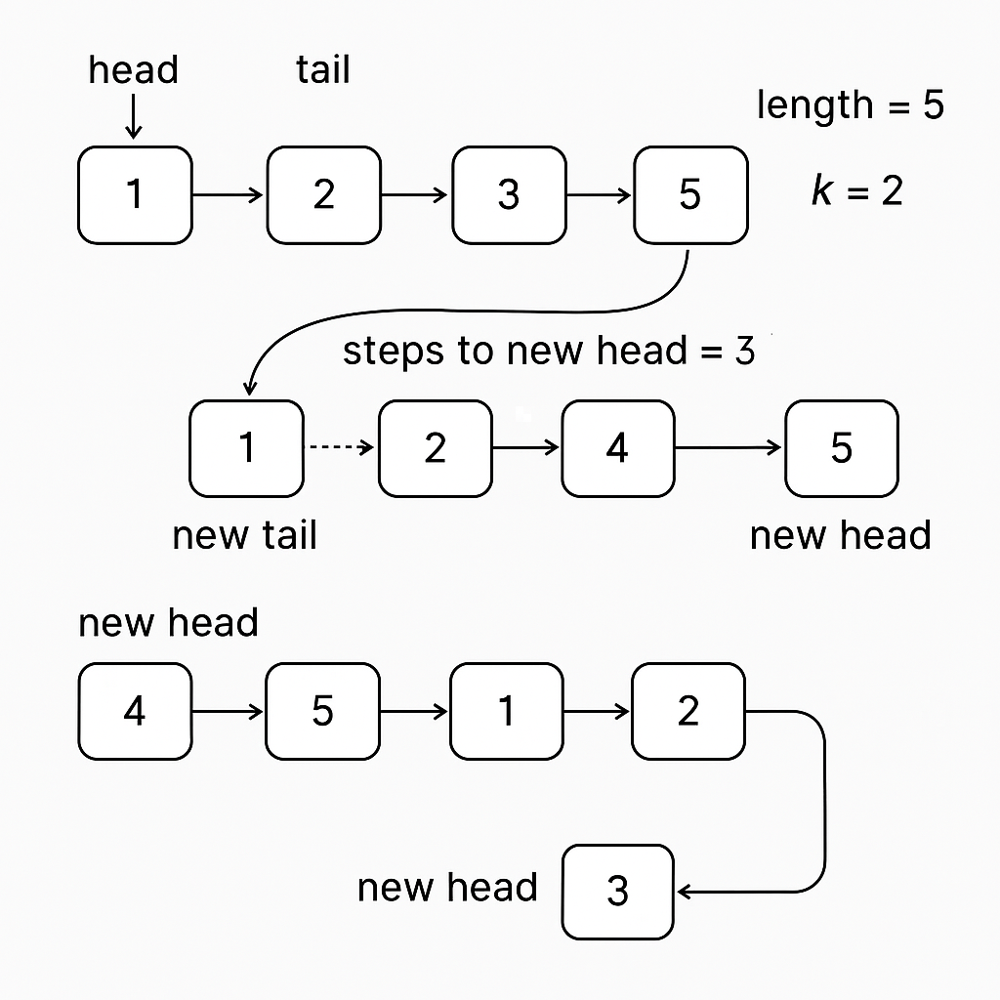
![head = [1,2,3,4,5], k = 2](../assets/data_structures/ll_rotate_ex1.jpg)
![head = [0,1,2], k = 4](../assets/data_structures/ll_rotate_ex2.jpg)